三角形 の 角度 を 求める 423647-三角形の角度を求める問題

直角三角形の底辺と角度から、高さ・斜辺・面積を計算します。 底辺と角度を入力し「高さ・斜辺・面積を計算」ボタンをクリックすると、入力された直角三角形の高さと斜辺と面積が表示されます。 底辺a： 角度θ： 度 ラジアン 底辺aが1、角度θが30°の直角三角形 高さ b： 斜・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。 sin(サイン)から角度 cos(コサイン)から角度解説 三角比というのは，与えられた角度に対して，ただ1つ値が決まるもので，その角度が「どんな形の三角形の角の大きさであるか」にはよらないからです。 この話を考えるとき，三角比の 「値を求める」 のか， 「値を利用する」 のかを区別して考えてみましょう。

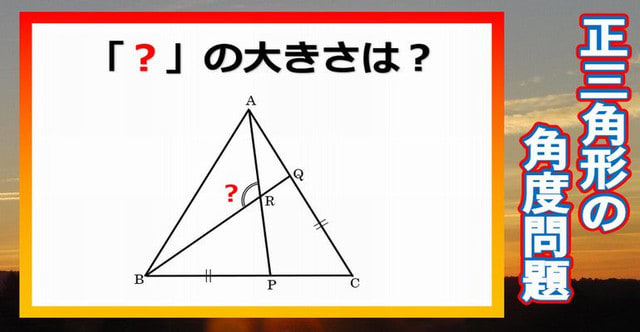
正三角形の角度問題 シンプルですが面白い 脳トレにはちょうど良い問題です 暇つぶしに動画で脳トレ

三角形の角度を求める問題

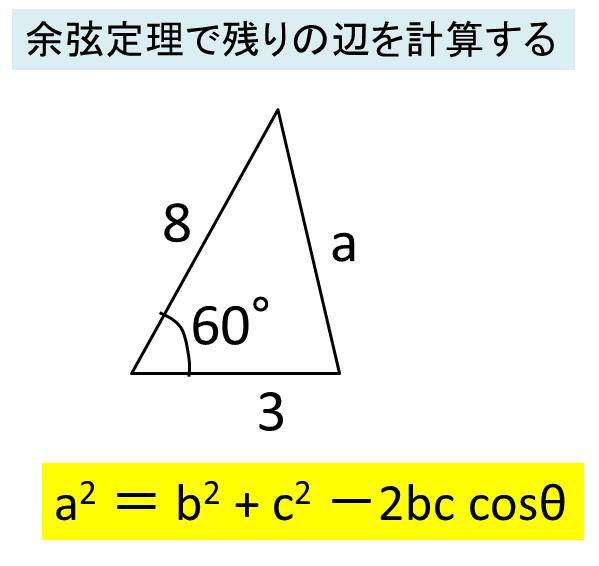
三角形の角度を求める問題- 三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦（cos(コサイン)）を求める。 わからないのは角度なので すべて余弦定理 で計算することができます。 例題： の三角形の∠A,B,Cを求める。 答え 余弦定理より よってA=60° 余弦定理より よってC=45° , B=180°60°45°=75° cos75°の値を知っていればcosBの値からBを求めることができます。 ですがこのページを読んでいる段階ではまだ知らないという前提にしてます。 逆に知らなかった人は この計算

この二等辺三角形の角度を求めてください この三角形は Ab Acの二等辺 Okwave

正弦定理から，三角形の辺の長さを求める計算について ABCにおいてa = 3 ，A = 60°，B = 45°のときbを求めよ。 という問題がありますが， これを定理にあてはめていって， b = 3 / sin60°× sin45° まではつくれるんですが，そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが，意味がわかり 直角三角形の角度θの求め方について質問です。 ※三角形の内角は30°60°90°です。 斜辺の長さがわからない時のθの求め方として、｢tanθ=底辺a×高さb｣の公式を使うと思うのですが、この公式ですとθが30°では なく33°になってしまいます。 Tanθ=1/√3≒0577rad radを度に変換する。 5732°(1radの値)×0577=33° この三角形は単位円が半径1であることと、交点のy座標が であることから辺の比を求めることができます。 今回できた三角形は の三角形であるため、30°、60°,90°の三角形であることがわ

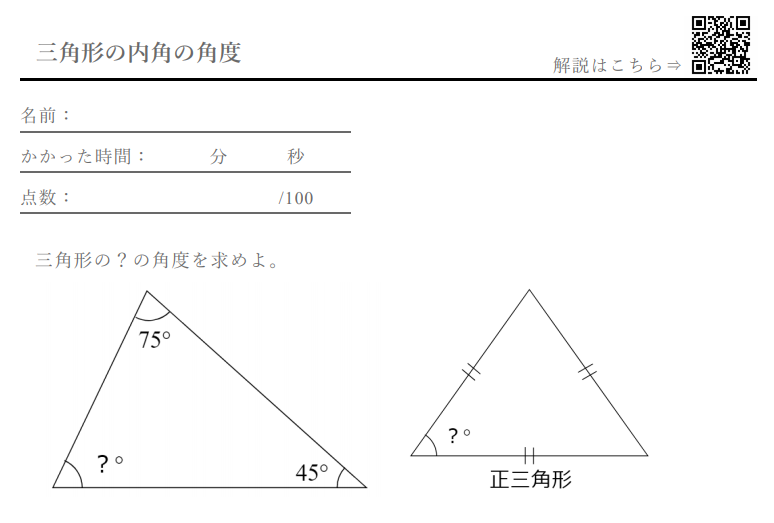
答えの度分秒（° ′ ″ ）は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos ⁡ θ = a c , sin ⁡ θ = b c , tan ⁡ θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。逆三角関数にはアークサイン（arcsin、逆正弦）、アークコサイン （arccos、逆余弦）、アークタンジェント（arctan、逆正接）があり、下の図 の直角三角形ABCの例を使えば、次のように定義されます。 θ＝arcsin θ＝arccos θ＝arctan

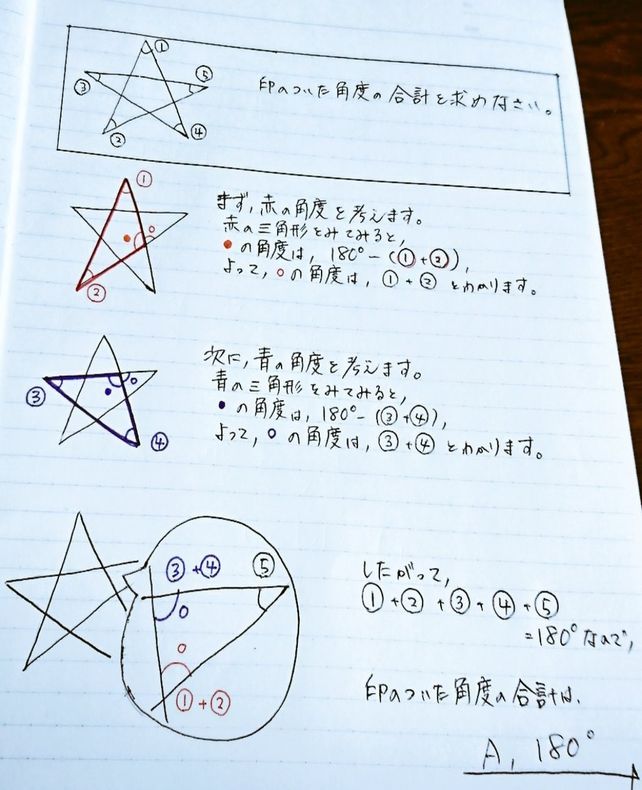
 三角形の内接円、外接円、面積、角度 外接円の中心と半径を求めるコードを作ってみました。 公式がわからなかったので、 Wikipedia の外接円の項目を参照しました。 (x1)^2 (y2)^2=3^2という円の方程式の形で結果を出力します。 小数の場合は小数点以下2桁文字なら、「方程式を立式しよう！ 」ってすぐに思いますよね。 や でも、立式してしまえばいいのです。 下の図の赤い三角形に着目して 、 ( )×250 = 180 ( ) × 2 50 = 180 より、 = 65 = 65 ・・・① 青い三角形に着目して、 x = 180 x = 180 ・・・② ①、②を見比べてみましょう。 = 65 = 65 ・・・① x = 180 x = 180 ・・・②三角比の値から角度を求める問題が出てきたら、直角三角形の図をイメージしよう。 sinθ＝（高さ）/（斜辺） cosθ＝（底辺）/（斜辺） tanθ＝（高さ）/（底辺） の関係から、直角三角形をイメージすれば、角度θが求められるね。 そして θの範囲 にも注目しよう。 0°≦θ≦180° のときは、 座標平面の上半分 、 分度器 の範囲で考えるんだ。

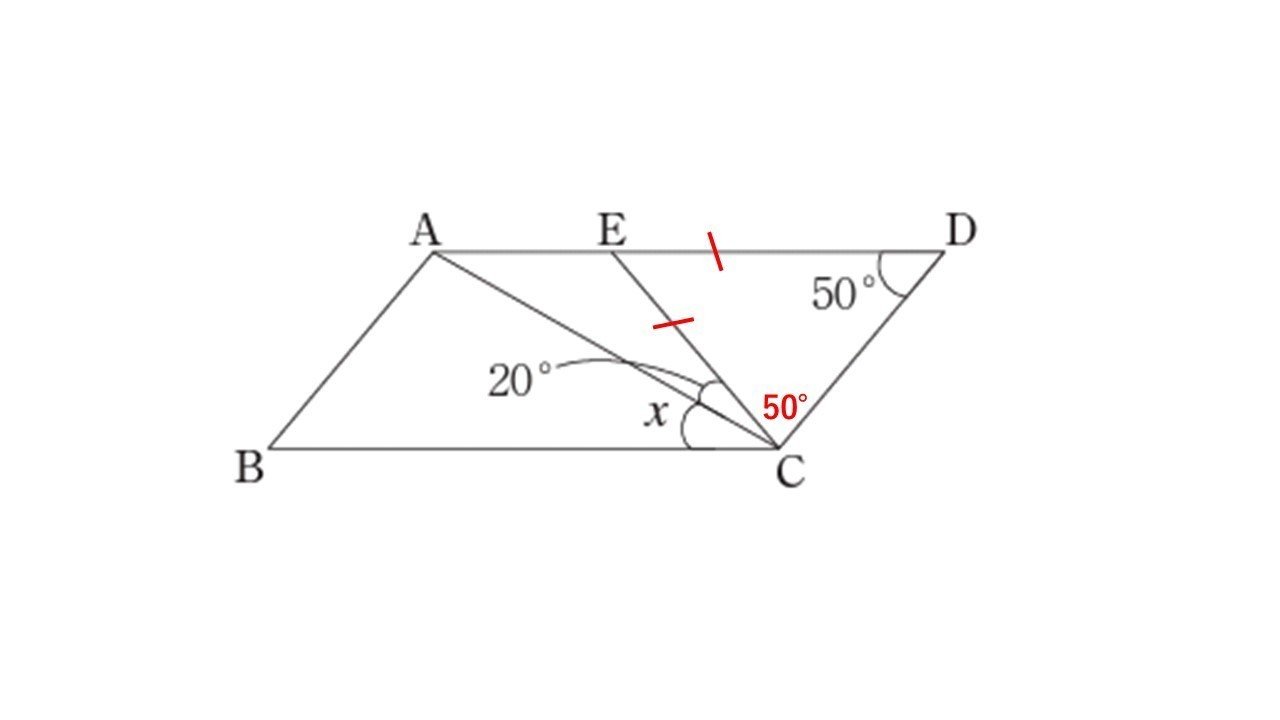
中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note

1

直角三角形を描画し、その角度を求めるということをしようとしています。 (各点はランダムで出しますが必ずどこかひとつの角が直角になるようにします。) 三角形の2辺の長さと直角ということを利用し、残りの角のひとつを出したいと考えています。 やり方として、三平方の定理で角度をよって、三角形の内角をすべて足したら180°になることから $$x=180(7070)=40°$$ となります。 外角が与えられた場合には そこをたどって、二等辺三角形の内角を求めていくと 答えに近づくことができますね(^^) 三角形の角度を求める問題です。ごく基本的な問題なので、確実に出来るようにしましょう。ポイント 三角形の内角の和は180度 内角と外角はどこか 三角形の1つの外角は、となりあっていない2つの内角の和に等しいこの3つのことを教科書などでしっかり確認してから問題に取り組んでく

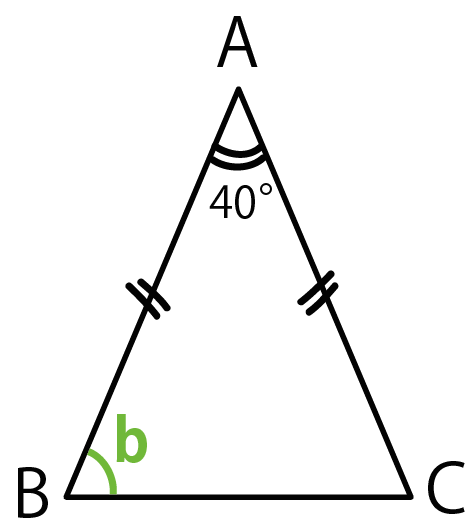
簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典

センター問題 (2) 三角形を解くとは 三角形には3つの角と3つの辺があります．これらの内の幾つかの要素が与えられたとき，残りの要素を求めることを「 三角形を解く 」といいます． 相似図形の性質を考えると分かるように，三角形が決まるためには 三角形の内角の和は180°なので、この四角形の内角の和は180°×2＝360°になります。 ですのでAの角度は、360°(72°38°30°)＝2° よって、 答え A＝2 °つの角度が決まれば，三角形の辺の長さの比も決まるのである．そこで，直角三角形の辺同士の長さ の比と角度との関係を定義し，様々な計算の助けとしている．これが三角比(trigonometric ratio) で あり，三角関数へと発展する． A B a C b c q 上図において，斜辺と底辺とのなす角度をθ とすれば

図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に

紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター

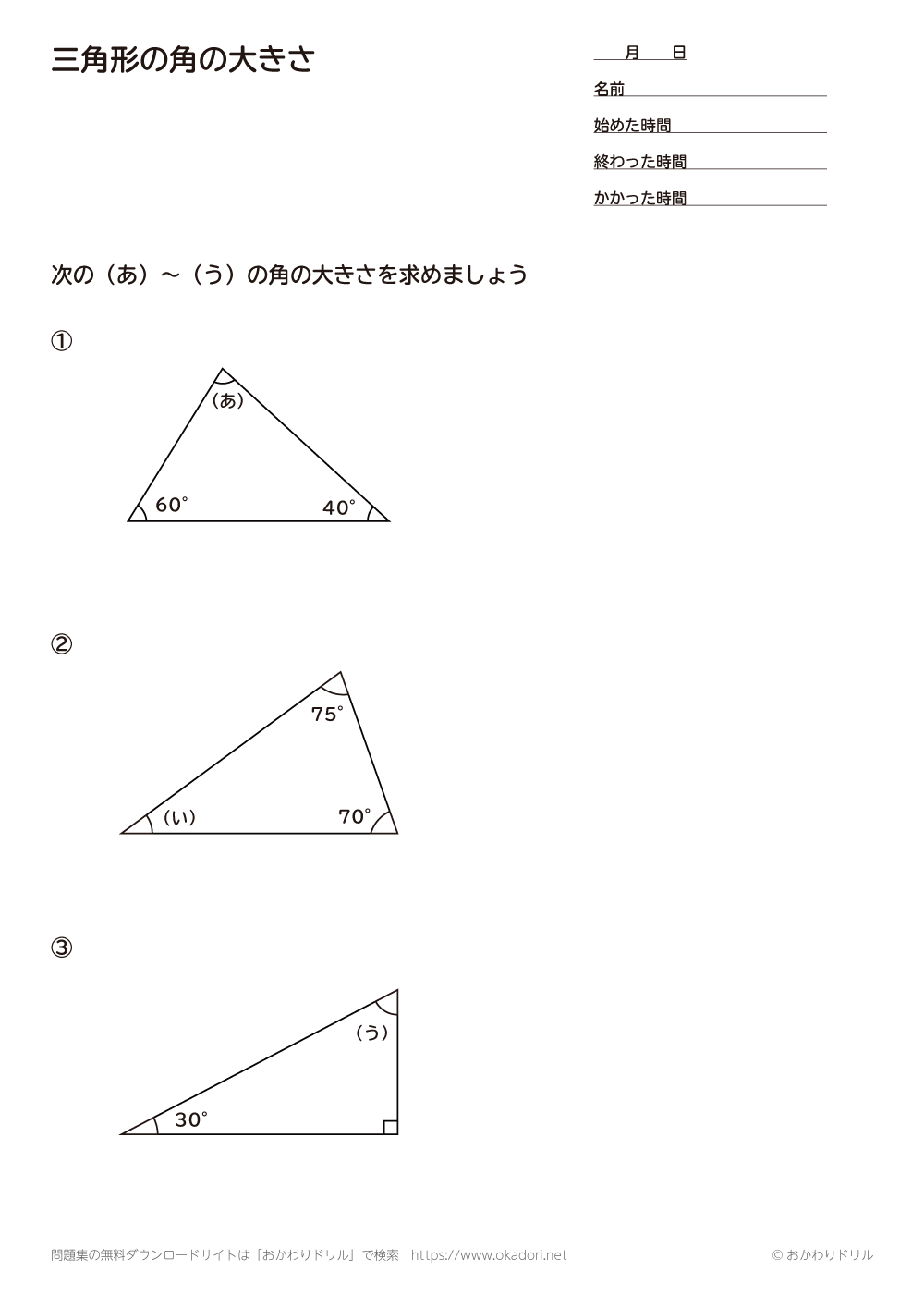
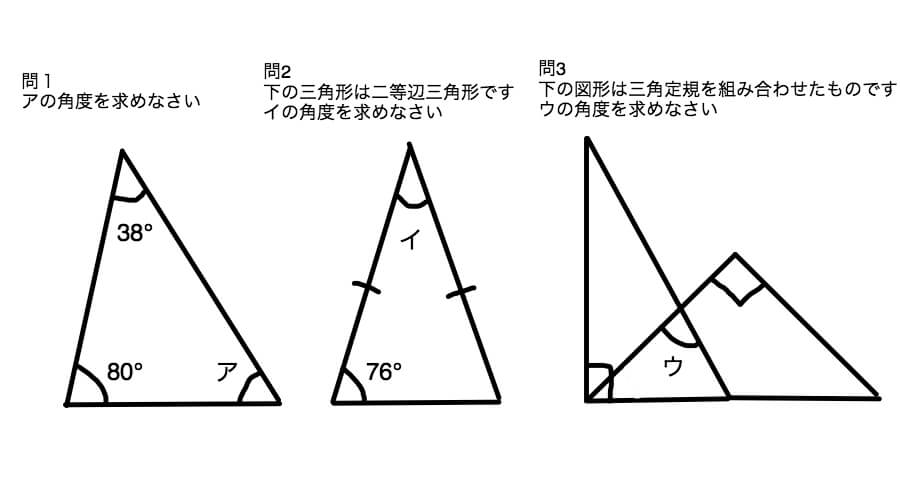
 二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう！ 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な下の三角形で，ア，イの角度を求めなさい。 （1） （2） （1）30°＋50°＝80° 答え 80° （2）角イ＋70°＝145° 角イ＝145°－70° ＝75° 答え 75° 下の図の三角形について，ア，イの角度を求めてみよう。 アの角度を求めると， 角ア＝180°－（80°＋40°） ＝60° 角アが60°であることを使ってイの角度を角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和＝180度 となるのです。

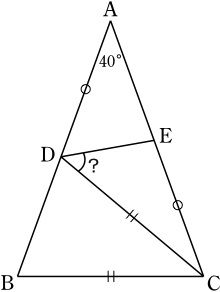
二等辺三角形の頂角を求める問題の 逆 の問題 東大合格コム

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

 （1）三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 では、円周の長さを求める公式を思い出してほしい。「直径×円周率」である。小学校なので円周率はπではなく314としておこう。 さて 問、弧abの長さを求めなさい。 弧の長さを求める問題だ。あーあったあった。 見ての通り円と二等辺三角形は密接な関係がある。半径が等辺になった三角形の面積を求める公式は「 ×高さ÷2」。 に入る言葉は何？（底辺、斜辺、周囲、角度) のクイズの答えは（）から選択してください。 クイズプラスは、多くの問題を記載しているクイズブログです。

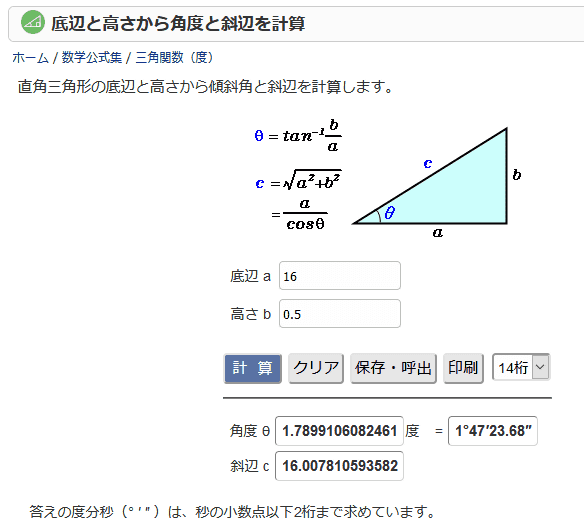
表計算ソフトを使って 底辺 と 高さ から 角度 を求める

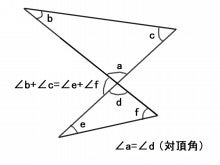
角度の求め方 数学が嫌いなんです

ることを活用して，三角形の 色々な角度を計算で求める。 考三角形の内角の和を，三角 定規の角の大きさを調べた り，いろいろな三角形の三 つの角を一つの点に集めた りすることを通して帰納的 に考え，説明している。 (ノート・観察) 技計算で三角形の角の大き さを求めることができる余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます： a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 （正確には、角 A そのものではなく cos A が求まりますが二等辺三角形の角度の求め方（計算） 色々な二等辺三角形の角度を求めましょう。下図をみてください。頂角が90度です。前述した計算式を使います。 α2θ＝180 902θ＝180 2θ＝90 θ＝45 頂角が直角の二等辺三角形を、直角二等辺三角形といいます。次の問題です。低角が60度のとき、頂角を計算しましょう。

外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三角関数の角度を計算する場合、「エクセル」を使うと便利です。 θ＝Arcsin (038)のような半端な辺の比に対する角度も計算できます。 まずエクセルのセルに「= ASIN (038)」と入力してください。S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2) i f a ≥ b, c h = 2 S a, B二等辺三角形や正三角形で，1つの角の角度を計算で求める方法を教えて 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author VAIO Created Date 216 PM

中2 数学 4 2 三角形の角度の利用 Youtube

三角形の角度を求める問題 小学生 中学生の勉強

直角三角形の解法 直角三角形 それでは実際に直角三角形の解法をしてみましょう。ここでは、具体的に次のような直角三角形を考え、分かっていない残りのB, a, bを求めたいと思います。 角Bの値 まずは、角度Bは簡単に求まります。三角形の内角の和は180 二等辺三角形の角度を求める基本問題！ では、まずは基本問題からみていこう！ 次の\(∠x\)を求めなさい。 ゆい お、これは簡単です！ 底角が同じなこと 三角形の角は全部で180° ってことを使えばいけますね★ その通りですね！ まずは、底角が等しいことから このように角度が分かり水平面 (XY 平面) に対する三角形 (を含む平面) の傾き (角度，方向)．(3次元のみ) 三角形の法線ベクトル (3点を含む面に垂直なベクトル)．(3次元のみ) Triangle2Dxls (2次元用) \308 Triangle3Dxls (3次元用) \514 2次元用 ＋ 3次元用 (セット割引) \617 Triangle2Dxls (2次元用) Triangle3Dxls (3次元用) 8．サンプル

ちょうちょ型図形の角度は 求め方を徹底解説 数スタ

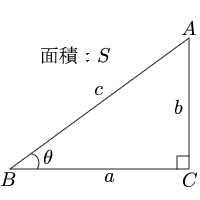
直角三角形 斜辺と角度 三角形の計算 計算サイト

答えは， ∠BAD = 30° ∠ B A D = 30 ° となります． この \(2\) つを押さえておけば、単位円の中に直角三角形を配置するだけで、主要な角度の三角比を求めることができます。 角度は、度数・ラジアンのどちらでも書けるようにしっかり覚えておきましょう！ 三角関数の変換公式 ここでは、三角関数の角度の変換公式（\(90^\circ −

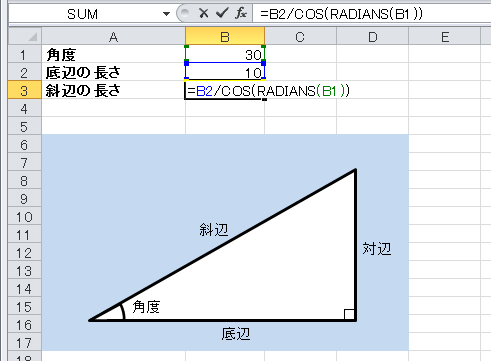
角度からコサインを計算するには Cos Radiansの解説 エクセル関数リファレンス

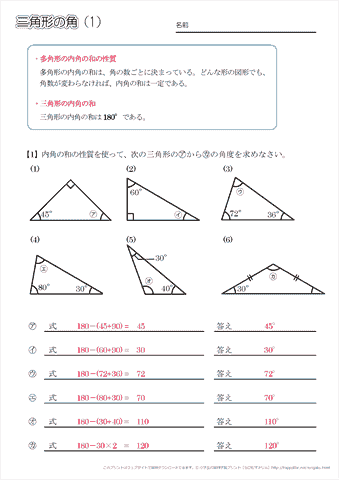
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学

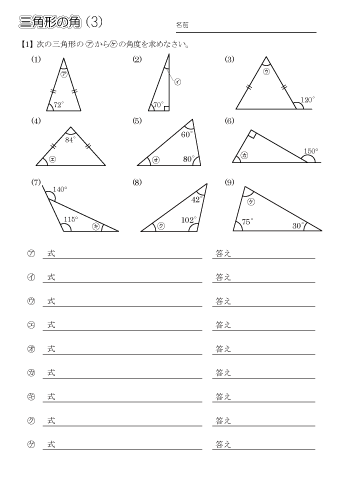
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

三角形の角度を求める問題がわかりません 三角形の和と直線の角度 Yahoo 知恵袋

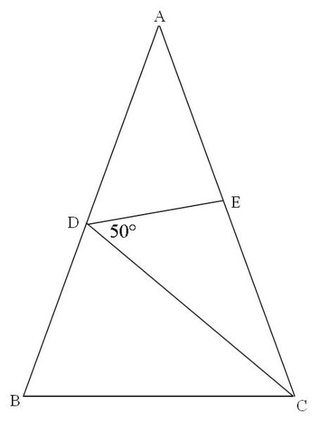
二等辺三角形の頂角を求める問題 難問 東大合格コム

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

この二等辺三角形の角度を求めてください この三角形は Ab Acの二等辺 Okwave

円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi

Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf

なつおの部屋 計算ソフト フレーム ６ 直角のない三角形の角度計算

角度を計算する方法 9 ステップ 画像あり Wikihow

角度を求める問題 中学受験 田中貴 Com

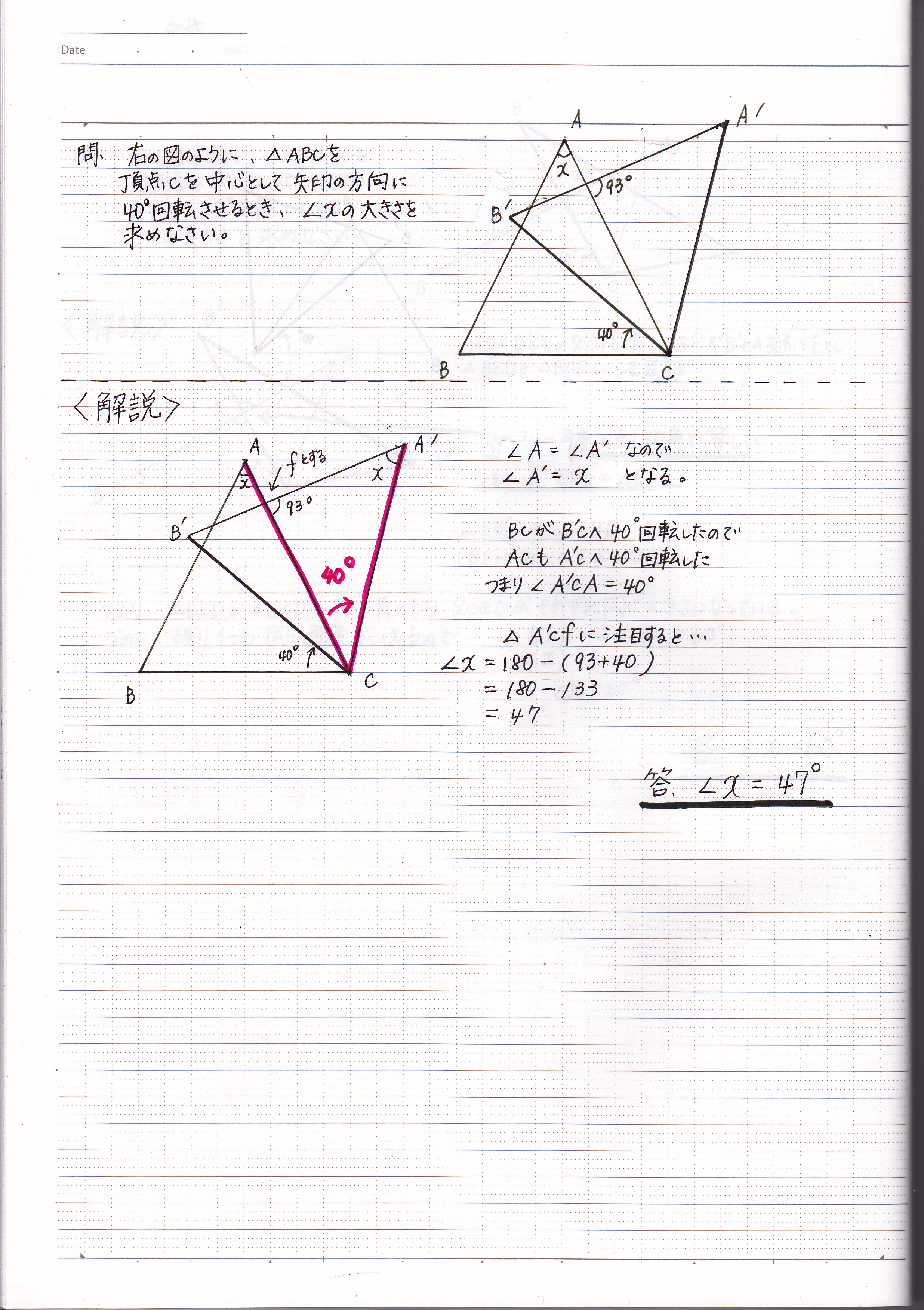
回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方

小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル

ラングレーの問題 整角四角形

角度の求め方 角度の求め方 Mqttk

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

図形の角度 三角形 小5 小6 プリントok

正三角形の角度問題 シンプルですが面白い 脳トレにはちょうど良い問題です 暇つぶしに動画で脳トレ

三角形の角度を求める 思考力を鍛える数学

Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める

二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト

1

三角形の辺から角度を計算 製品設計知識

ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

中学受験 小学4年生予習シリーズ算数 第8回 三角形の角 基本知識と解くコツ

二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明

二等辺三角形の角度 無料で使える中学学習プリント

２ 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に

三角形 の内角の角度 計算ドリル 問題集 数学fun

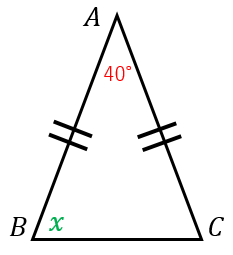
二等辺三角形の角度の求め方と例題 具体例で学ぶ数学

算数 数学パズル 解答 ー 三角形の角度を求める ー ミスター ビーンのお気楽ブログ

普通の電卓で計算できる直角三角形の近似計算

角度の問題まとめ 無料で使える中学学習プリント

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

1

数学 中2 53 角度チャレンジ Lv 1 Youtube

直角三角形公式角度 直角三角形 斜辺と角度 三角形の計算 計算サイト翻譯此網頁 Rzcpe

三角形の３辺から角度を計算 高精度計算サイト

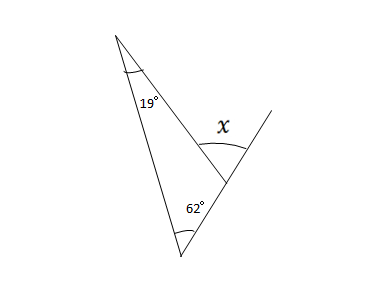
平行線と角度 7 ネット塾

直角三角形の解法 1

小５ 算数 小５ ３１ 三角形の角 Youtube

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

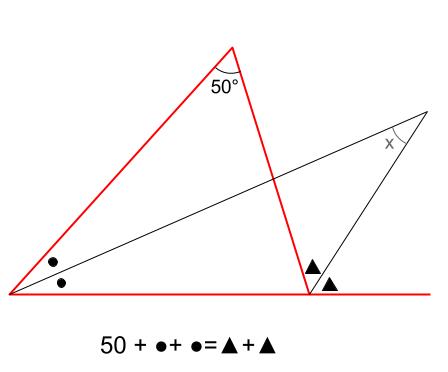
中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su

正確な角度の測定 割り付け

三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun

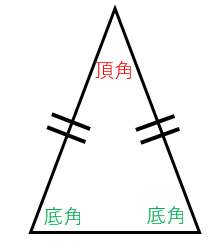
二等辺三角形の角度の求め方と例題 具体例で学ぶ数学

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

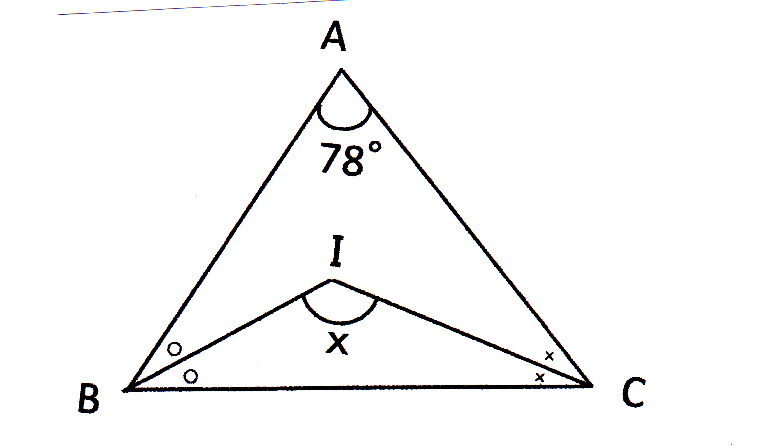
三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方

二等辺三角形の角を求める Youtube

直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo

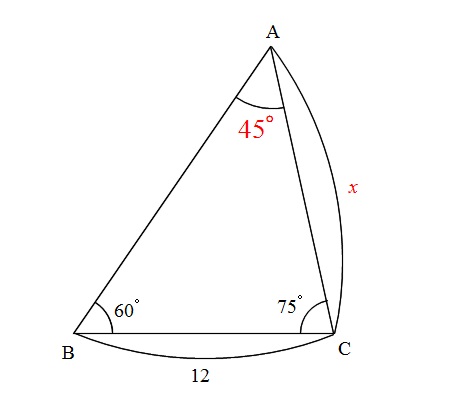
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット

底辺と高さから角度と斜辺を計算 高精度計算サイト

直角三角形の角度の求め方 教えて下さい 斜辺以外の２辺の長さが分かっ Yahoo 知恵袋

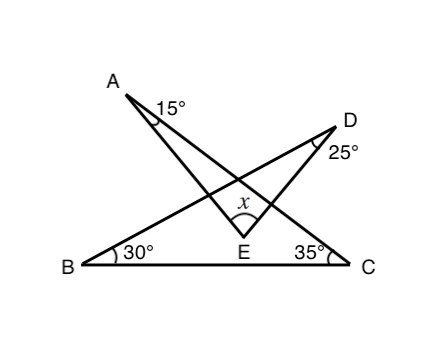
角度を求める問題 スリッパを探そう 苦手な数学を簡単に

角度の計算 裏技まとめ 教遊者

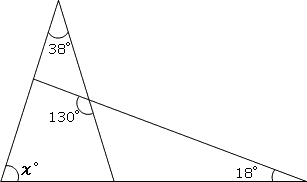
角度の求め方 算数の教え上手 学びの場 Com

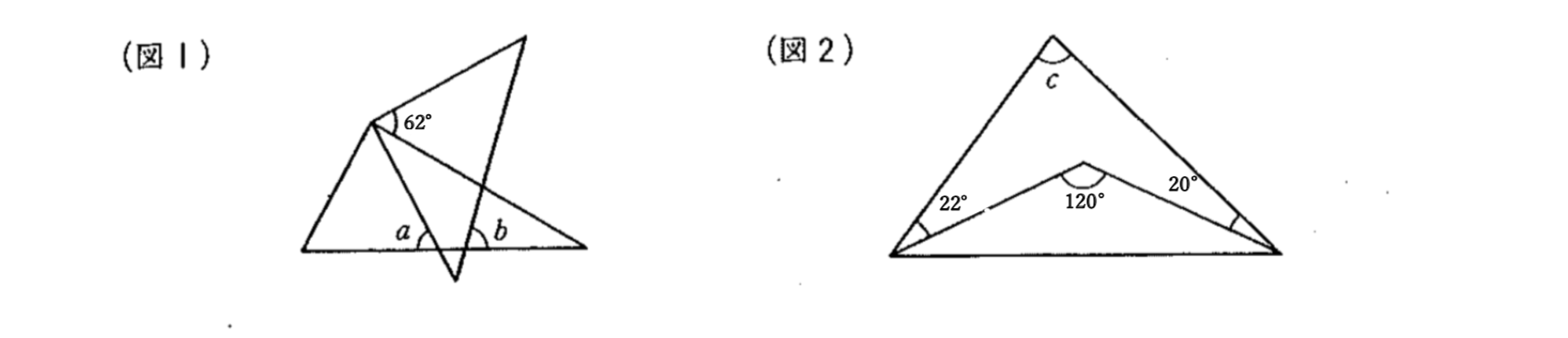
４ ３ 重なった２つの三角形から角度を求めるには さんすうがく

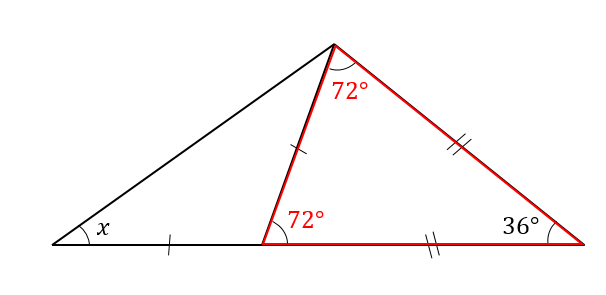
二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ

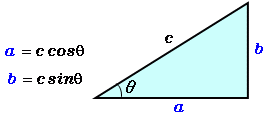
角度と斜辺から底辺と高さを計算 高精度計算サイト

Math 平行と合同 角の二等分線と角度 働きアリ

二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear

正三角形や二等辺三角形の内角 Youtube

高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット

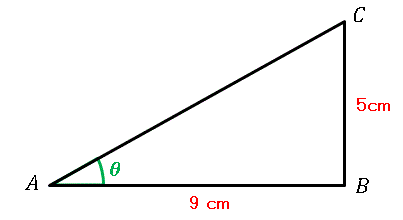
Excel で直角三角形の斜辺と底辺に挟まれた角度を求めます

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

15 5 15zazczdlczetp797 Descubre Como Resolverlo En Qanda

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

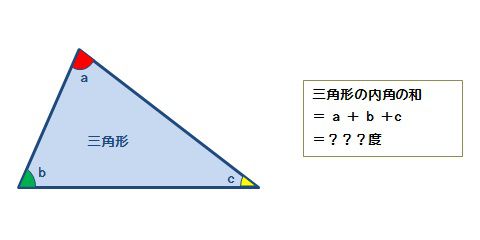
三角形の内角の和 算数の公式覚えてますか

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ

算数の問題でもあり 数学の問題でもありますの解答解説１ 角度を求める問題7月19日出題 Fitのひろば

余弦定理で角度を求める方法 数学の星

あ かまでの角度を求めてください 急いでます 教えてください Clear

三角形の角度を求める問題 小学生 中学生の勉強

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

円と三角形 角度 中学から数学だいすき

角度の求め方 算数の教え上手 学びの場 Com

小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

タンジェントとは何か 中学生でも分かる三角関数の基礎

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

角度の難問 中学生版

角度の求め方 算数の教え上手 学びの場 Com

Incoming Term: 三角形の角度を求める, 三角形の角度を求める問題, 三角形の角度を求める公式, 三角形の角度を求める プリント,